For decades, research in distributed systems, especially in Byzantine consensus and state machine replication (SMR), has focused on two main goals: consistency and liveness. Consistency means all nodes agree on the same sequence of transactions, while liveness ensures the system continues to add new ones. Still, these properties do not stop bad actors from changing the order of transactions after they are received.
In public blockchains, that gap in traditional consensus guarantees has become a serious problem. Validators, block builders or sequencers can exploit their privileged role in block ordering for financial gain, a practice known as maximal extractable value (MEV). This manipulation includes profitable frontrunning, backrunning and sandwiching of transactions. Because transaction execution order determines validity or profitability in DeFi applications, the integrity of transaction ordering is vital for maintaining fairness and trust.
To address this critical security gap, transaction order-fairness has been proposed as a third essential consensus property. Fair-ordering protocols ensure that the final order of transactions depends on external, objective factors, such as arrival times (or receiving order) and is resistant to adversarial reordering. By limiting how much power a block proposer has to reorder transactions, these protocols move blockchains closer to being transparent, predictable, and MEV-resistant.
The Condorcet paradox and impossibility of ideal fairness
The most intuitive and strongest notion of fairness is Receive-Order-Fairness (ROF). Informally defined as “first received, first output,” ROF dictates that if a sufficient number of transactions (tx) arrive at a majority of nodes earlier than another transaction (tx′), then the system is required to order tx before tx′ for execution.
However, achieving this universally accepted “order fairness” is fundamentally impossible unless it is assumed that all nodes can communicate instantaneously (i.e., operating in an instant synchronous external network). This impossibility result stems from a surprising connection to social choice theory, specifically the Condorcet paradox.
The Condorcet paradox illustrates how, even when every individual node maintains a transitive internal ordering of transactions, the collective preference across the system can result in what are known as non-transitive cycles. For example, it is possible that a majority of nodes receive transaction A before B, a majority receive B before C, and a majority receive C before A. Hence, the three majority preferences form a loop (A→B→C→A). This means that no single, consistent ordering of the transactions A, B and C can ever satisfy all majority preferences simultaneously.
This paradox demonstrates why the goal of perfectly achieving Receive-Order-Fairness is impossible in asynchronous networks, or even in synchronous networks that share a common clock if external network delays are too long. This impossibility necessitates the adoption of weaker fairness definitions, such as batch order fairness.
Hedera Hashgraph and flaw of median timestamping
Hedera, which employs the Hashgraph consensus algorithm, seeks to approximate a strong notion of receive-order fairness (ROF). It does this by assigning each transaction a final timestamp computed as the median of all nodes’ local timestamps for that transaction.
However, this is inherently prone to manipulation. A single adversarial node can deliberately distort its local timestamps and invert the final ordering of two transactions, even when all honest participants received them in the correct order.
Consider a simple example with five consensus nodes (A, B, C, D and E) where Node E acts maliciously. Two transactions, tx₁ and tx₂, are broadcast to the network. All honest nodes receive tx₁ before tx₂, so the expected final order should be tx₁ → tx₂.
In this example, the adversary assigns tx₁ a later timestamp (3) and tx₂ an earlier one (2) to skew the median.
When the protocol computes the medians:
-
For tx₁, the timestamps (1, 1, 4, 4, 3) yield a median of 3.
-
For tx₂, the timestamps (2, 2, 5, 5, 2) yield a median of 2.
Because the final timestamp of tx₁ (3) is greater than that of tx₂ (2), the protocol outputs tx₂ → tx₁, thus reversing the true order observed by all honest nodes.
This toy example demonstrates a critical flaw: The median function, while appearing neutral, is paradoxically the actual cause of unfairness because it can be exploited by even a single dishonest participant to bias the final transaction order.
As a result, Hashgraph’s often-touted “fair timestamping” is a surprisingly weak notion of fairness. The Hashgraph consensus fails to guarantee receive-order fairness and instead depends on a permissioned validator set rather than on cryptographic guarantees.
Achieving practical guarantees
However, to circumvent the theoretical impossibility demonstrated by Condorcet, practical fair-ordering schemes must relax the definition of fairness in some way.
The Aequitas protocols introduced the criterion of Block-Order-Fairness (BOF), or batch-order-fairness. BOF dictates that if sufficiently many nodes receive a transaction tx before another transaction tx′, then tx must be delivered in a block before or at the same time as tx′, meaning no honest node can deliver tx′ in a block after tx. This relaxes the rule from “must be delivered before” (the requirement of ROF) to “must be delivered no later than”.
Consider three consensus nodes (A, B and C) and three transactions: tx₁, tx₂, and tx₃. A transaction is considered “received earlier” if at least two of the three nodes (a majority) observe it first.
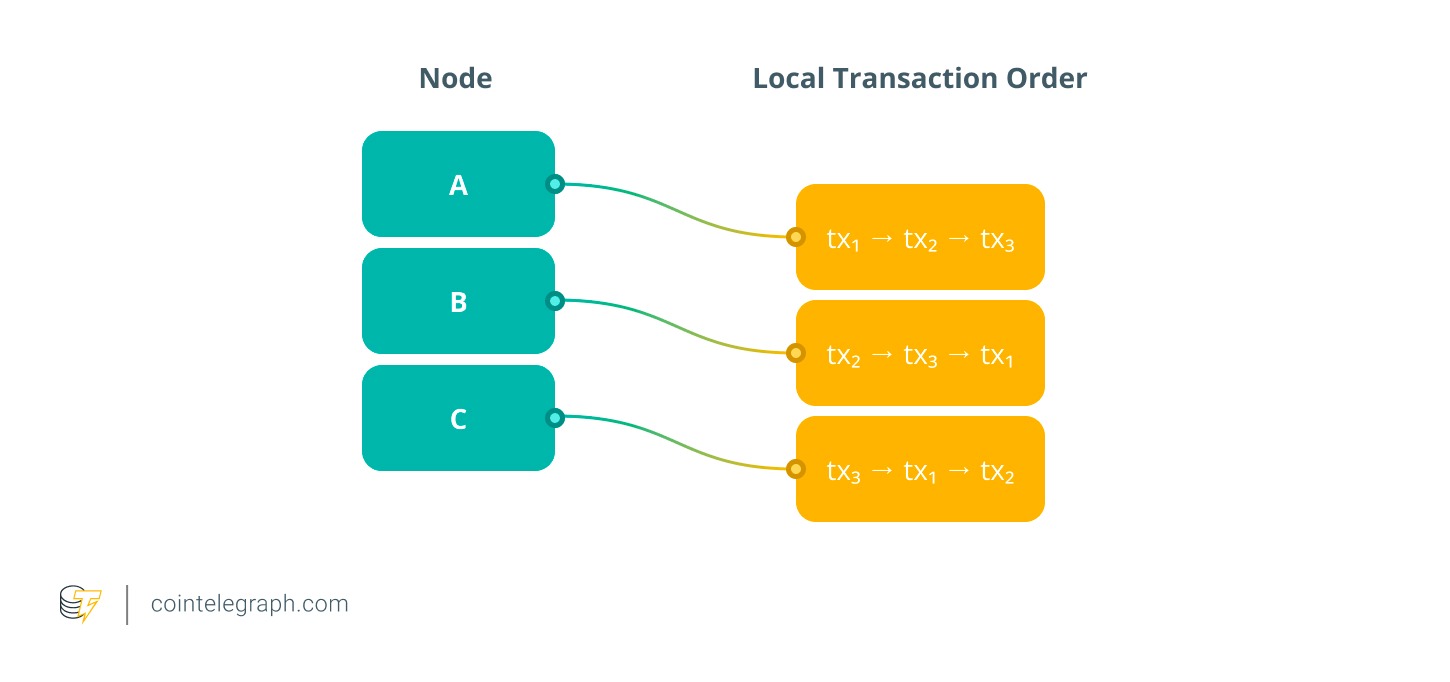
If we apply majority voting to determine a global order:
-
tx₁ → tx₂ (agreed by A and C)
-
tx₂ → tx₃ (agreed by A and B)
-
tx₃ → tx₁ (agreed by B and C)
These preferences create a loop: tx₁ → tx₂ → tx₃ → tx₁. In this situation, there’s no single order that can satisfy everyone’s view at once, which means strict ROF is impossible to achieve.
BOF solves this by grouping all the conflicting transactions into the same batch or block instead of forcing one to come before another. The protocol simply outputs:
Block B₁ = {tx₁, tx₂, tx₃}
This means that, from the protocol’s perspective, all three transactions are treated as if they happened at the same time. Inside the block, a deterministic tie-breaker (such as a hash value) decides the exact order in which they’ll be executed. By doing this, BOF ensures fairness for every pair of transactions and keeps the final transaction log consistent for everyone. Each one is processed no later than the one that precedes it.
This small but important adjustment lets the protocol handle situations where transaction orderings conflict, by grouping those conflicting transactions into the same block or batch. Importantly, this does not result in a partial ordering, as every node must still agree on one single, linear sequence of transactions. The transactions inside each block are still arranged in a fixed order for execution. In cases when no such conflicts occur, the protocol still achieves the stronger ROF property.
While Aequitas successfully achieved BOF, it faced significant limitations, particularly that it had very high communication complexity and could only guarantee weak liveness. Weak liveness implies that a transaction’s delivery is only guaranteed after the entire Condorcet cycle it is a part of is completed. This could take an arbitrarily long time if cycles “chain together.”
The Themis protocol was introduced to enforce the same strong BOF property, but with improved communication complexity. Themis achieves this using three techniques: Batch Unspooling, Deferred Ordering, and Stronger Intra-Batch Guarantees.
In its standard form, Themis requires each participant to exchange messages with most other nodes in the network. The amount of communication required increases with the square of the number of network participants. However, in its optimized version, SNARK-Themis, nodes use succinct cryptographic proofs to verify fairness without needing to communicate directly with every other participant. This reduces the communication load so that it grows only linearly, which allows Themis to scale efficiently even in large networks.
Assume five nodes (A–E) participating in consensus receive three transactions: tx₁, tx₂, and tx₃. Due to network latency, their local orders differ:
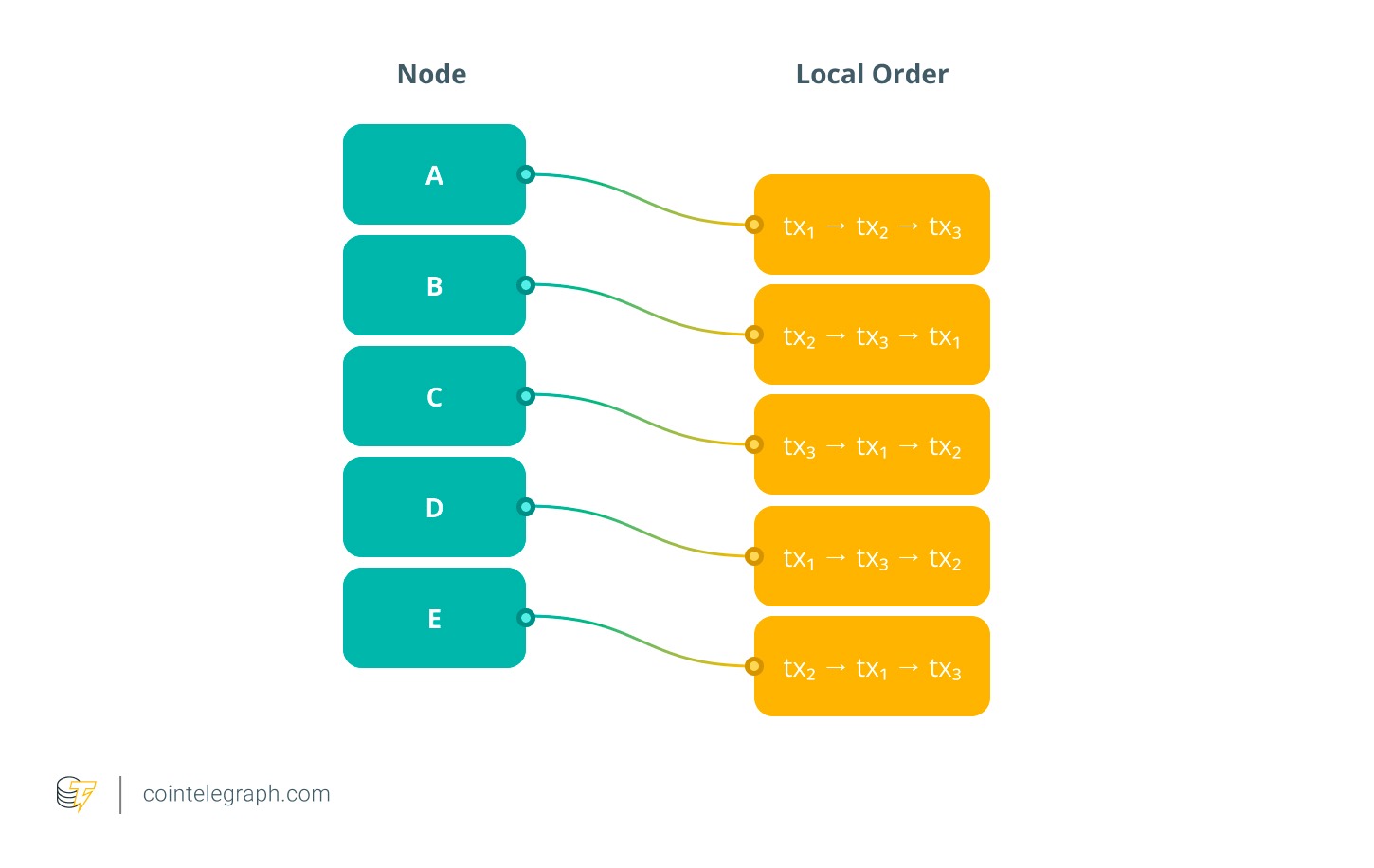
As in Aequitas, these preferences create a Condorcet cycle. But instead of waiting for the entire cycle to be resolved, Themis keeps the system moving using a method called batch unspooling. It identifies all transactions that are part of the cycle and groups them into one set, called a strongly connected component (SCC). In this case, all three transactions belong to the same SCC, which Themis outputs as a batch-in-progress, labeled Batch B₁ = {tx₁, tx₂, tx₃}.
By doing this, Themis allows the network to keep processing new transactions even while the internal order of Batch B₁ is still being finalized. This ensures the system stays live and avoids stalling.
Overview:
The concept of perfect fairness in transaction ordering may seem straightforward. Whoever’s transaction reaches the network first should be processed first. However, as the Condorcet paradox demonstrates, this ideal cannot hold in real, distributed systems. Different nodes see transactions in different orders, and when those views conflict, no protocol can build a single, universally “correct” sequence without compromise.
Hedera’s Hashgraph tried to approximate this ideal with median timestamps, but that approach relies more on trust than on proof. A single dishonest participant can distort the median and flip transaction order, revealing that “fair timestamping” is not truly fair.
Protocols like Aequitas and Themis move the discussion forward by acknowledging what can and cannot be achieved. Instead of chasing the impossible, they redefine fairness in a way that still preserves order integrity under real network conditions. What emerges is not a rejection of fairness, but its evolution. This evolution draws a clear line between perceived fairness and provable fairness. It shows that true transaction-order integrity in decentralized systems cannot depend on reputation, validator trust or permissioned control. It must come from cryptographic verification embedded in the protocol itself.
This article does not contain investment advice or recommendations. Every investment and trading move involves risk, and readers should conduct their own research when making a decision.
This article is for general information purposes and is not intended to be and should not be taken as legal or investment advice. The views, thoughts, and opinions expressed here are the author’s alone and do not necessarily reflect or represent the views and opinions of Cryptox.
Cryptox does not endorse the content of this article nor any product mentioned herein. Readers should do their own research before taking any action related to any product or company mentioned and carry full responsibility for their decisions.




